Simple and Compound Interest

Let’s begin by looking at simple interest, and then see how banks extend this idea to everyday business. First, what does it mean to invest a principal amount of money P in a bank at a simple interest rate r? The bank’s customers are letting the bank use their money for a period of time, and in return the bank is willing to return their original amount at the end of the period plus extra money called Interest. The amount of extra money depends on the interest rate that the bank pays and the period of time.
If Mrs. Hamlisch puts $200 into a savings account at the beginning of the year at 12% interest rate, at the end of the year her account will have $200 plus the interest that she earned. This interest is 12% of $200, or, from the simple interest formula I = Prt, I = (0.12)200 = 24.
At the end of the year she will have $200 + $24 = $224 in her bank account.
SIMPLE INTEREST FORMULA
If a principal amount P is invested at an interest rate r for t years, then the simple interest earned will be I = Prt.
We can use the simple interest formula to find a formula for the amount of money A that will be in a simple interest account after t years. The amount A is the original principal P plus the interest I earned over the period of time t.
A = P + I = P + Prt
To simplify the formula, factor P from the right-hand expression to obtain A = P + Prt = P(1 + rt).
-
EXAMPLE 1: Mr. Lablanc invests $500 at a simple interest rate of 6%. How much interest will he earn in one month? In six months? In one year?
Solution: The yearly interest he will earn is 6% of his original principal if he put his money in the bank for one year. However, in one month, he will only earn 1/12 of this amount.
The interest earned in one month is I = (500)(0.06)(1/12) = $2.50.
Similarly, in 6 months, the interest he will earn is I = (500)(0.06)( 6/12) = $15.
In one year the interest he will earn is I = (500)(0.06)(1) = $30.
Compare the three amounts of interest to see if they are reasonable. -
EXAMPLE 2: If you invest a principal P at an interest rate r compounded monthly, how much interest will P earn in one period?
Solution: Each period is one month long, so the length of time for one period is 1/12 of a year. The interest earned for one period will be I = P × r × ( 1/12). This is the same as we found in Example 1.
In general, if there are m periods in a year, the length of time for each period will be (1/m) of a year. The interest earned in one period will be I = P(r/m).
The periodic interest rate, then, is r/m. We can let I be the periodic interest amount and i = r/m. So the interest earned in one period Is I = Pi. That means the amount of money in an interest-earning account at the end of a period is P + Pi. This looks just like the simple interest formula except the interest rate r is replaced by the periodic interest rate i = r/m.
If an account earns interest compounded every six months, the periodic interest rate per each six-month period is i = 12%/2 = 6%. If the account earns interest compounded quarterly, or four times a year, the periodic interest rate is i = 12%/4 = 3%. Many accounts earn interest each month, so i = r/12.
-
EXAMPLE 3: Suppose we deposit $100 at 12% per year compounded monthly. How much will be in the account after three months? Find a formula for the amount in the account at the end of t months.
Solution: Let’s make a list of the amount of money in your account at the end of each of the first 3 months. Since one month is 1/12 of a year, the interest rate for one month is i = 0.12/12 = .01. The amount in the account after one month would be 100 + (.01)(100) = 100 + 1 = 101.
Let A(t) = amount in the account at the end of t months. So,
A(0) = 100 = P = amount in account at beginning of first month
A(1) = P + Pr = P(1 + i) = P(1.01) = amount in account at end of first monthNotice that we factor the P out of the sum producing the factor (1 + i). Computing the next two months, we get
A(2) = A(1) + A(1)i = A(1)(1 + i) = [P(1 + i)](1 + i) = P(1 + i)² = P(1.01)²
A(3) = A(2) + A(2)i = A(2)(1 + i) = [P(1 + i)²](1 + i) = P(1 + i)³ = P(1.01)³Month A(t) 0 $100.00 1 $101.00 2 $102.01 3 $103.03 4 $104.06
PROBLEM 1
Compute the total amount of money Mr. Lablanc will have in his account from Example 1.
Do this two ways:
1. Add the amount of interest earned to the initial amount. This is the total amount in the account after each time period.
2. Check your work by using the Simple Interest Formula for amount.
Most accounts set more than one interest period a year. This is called compounding. Financial institutions divide the year into a certain number of periods and add simple interest to an account after each period.
The pattern in Example 2 & 3 above works with different interest rates. The key idea is that for each period that passes, the amount at the end of the period is equal to the amount at the beginning of the same period multiplied by (1 + i), leading to the Compound Interest Formula.
COMPOUND INTEREST FORMULA
If an initial principal P is invested at an interest rate r compounded m times per year, then the amount in the account after n periods is A(n) = P(1 +i)^n, where i = r/m is the interest earned each year.
-
EXAMPLE 4: Sally invests $1,000 at 12% simple interest for three years. Ann invests $1,000 at a rate of 12% compounded monthly for three years.
-
How much money will Sally have after three years?
The amount that Sally will have is A = 1000(1 + 0.12 ∗ 3) = $1,360.
-
How much money will Ann have?
First, find the periodic interest rate: i = 0.12/12 = 0.01. Second, find the number of periods in three years. Because m = 12, there are 12 periods per year. In three years, there are 36 periods. Finally, use the compound interest formula to find Ann’s amount, using a calculator: A = 1000(1 + 0.12/12)^36 = $1,430.77.
-
Are you surprised by the results in any way?
Ann will have 1430.77 − 1360 = $70.77 more than Sally after 3 years.
-
If the time invested were ten years, by how much would the amounts differ?
Performing these calculations for ten years, Sally will have A = 1000(1 + .12 × 10) = $2,200. Ann will have A = 1000(1 + .01)^120 = $3,300.39. So after ten years, Ann will have $1,100.39 more than Sally.
-
PROBLEM 2
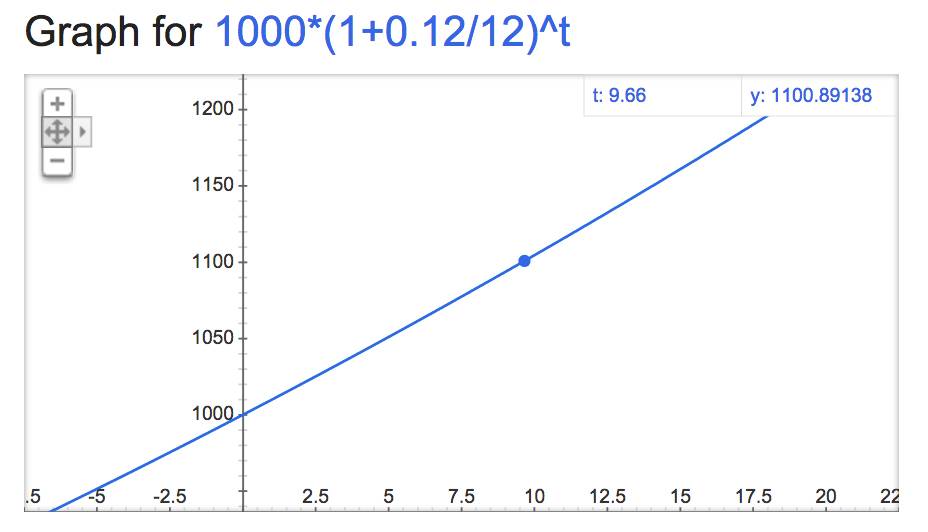
Suppose we deposit $1000 at 12% per year compounded monthly. How much will be in the account after six months? Find a formula for the amount in the account at the end of t months. Graph the function using your graphing calculator. Using the graph, estimate how many months it will take before you have $1,100.
Solution
We use the compound interest formula A(n) = P(1 + i)^n. Here i = r/m = 0.12/12, and n = 6 as each month is one period. So A(6) = 1000(1 + 0.12/12)^6 = 1061.52. So after six months there will be $1061.52 in the account.
The formula for the amount in the account at the end of t months is A(t) = 1000(1 + 0.12/12)^t. A graph of this function is plotted below. Using the graph, we see that it will be about 10 months for the account to reach $1,100.
Exercises
-
1. Sue invests $500 in the bank at a simple interest rate of 12%. How much interest will she earn after:
-
2. Chris invests $100 in the Simple Bank of America at a simple interest rate of 8%. How much will be in his account after:
-
3. When interest is compounded monthly, how many periods are there in:
-
4. Chris discovers he can invest his money in Texas Compound Bank. In that bank he can invest $100 at an interest rate of 8% compounded monthly. How much will be in his account after:
-
5. Jackie and Jennifer are sisters. On January 1, 1950, Jackie put $1000 in her safe and forgot about it. Her sister Jennifer only had $100 at that time. But she put her money into an account at the bank which paid 5% compounded yearly and forgot about it. On January 1, 2000, they decided to take out their money and throw a party. Who had more money to spend on the party, and how much more?
Jennifer has more, after fifty years she will have 100(1.05)^50 = $1146.74 due to earning interest. Jackie will have the same $1,000 sitting in her safe. Jennifer will have 146.74 more than her sister.
-
6. A bank offers three types of accounts. In the Bronze account, you earn 12% annual interest compounded monthly. In the Silver account, you earn 12.2% compounded twice a year. Finally, in the Gold account you earn 12.4% compounded once a year. If you deposit $100, how much will you have at the end of the year?
- Bronze: 100 x 1.01^12 = 112.68
- Silver: 100 x 1.061^2 = 112.57
- Gold: 100 x 1.124 = 112.40
-
7. How much money will Mr. Garza need to deposit into an account earning 12% per year (1% per month) compounded monthly in order to have $500 at the end of 3 years?
500/(1.01^36) = 349.46
-
8. John deposited $200 in the bank at a interest rate of 9% compounded monthly. How much will be in the account after 6 months?
200(1 + 0.09/12)^6 = 209.17
-
9. Victoria invests $100 at a simple interest rate of 8%. Penelope invests $100 at a rate of 8% compounded monthly. How much will each girl have after:
-
10. Using the simple interest formula A = P(1 + rt):
-
Solve for P
P = A/(1 + rt)
-
Solve for t
t = ((A/P) - 1)/r
-
-
11. Solve the compound interest formula A = P(1 + i)n for P
P = A/((1+i)^n)
-
12. Graph the following two functions: A = 100(1 + 0.08t) & A = 100(1 + 0.08/12)^(12t) Which function grows faster?
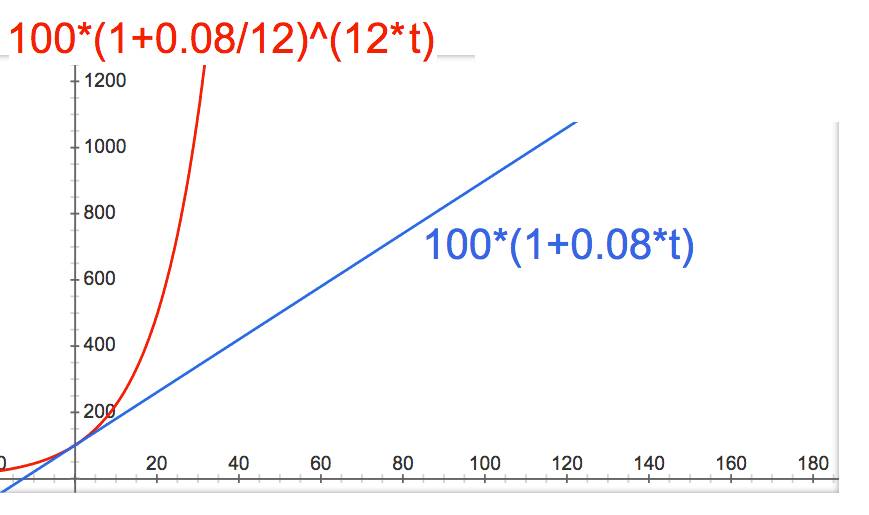
A = 100(1 + 0.08/12)^(12t) grows a lot faster, as shown in the graph above. The function plotted in red grows a lot faster.
